毕啸天，清华大学化工系博士。

经常有人在看完我这些文章之后会问我，你整天研究这些乱七八糟的东西有什么用？其实生活中我特别害怕面对这样一个问题。因为我也同样害怕我在生活中会变成一个要求别人去做有用的事情的人。我觉得本来一个单纯好玩的事在你要求它变得有用的时候，那一个瞬间它就变得不好玩了。

非常荣幸今天能站在一席的演讲台上。我叫毕啸天，现在是清华大学化学工程系的一名直博四年级的学生。因为我之前做过本科的辅导员，所以大家都叫我毕导。

大家可能之前有所耳闻，读博士、做科研的生活本身是比较单调的。但有时候我发现，当你把我放在这么一个相对单调的环境里面，我就特别喜欢用做科研的思维方式，去琢磨一些生活里面鸡毛蒜皮无聊的小事。

一、怎样才能抢到最大的红包？

给大家讲另外一个故事，是一个关于抢红包的故事，也是我自己做的一个小探究。春节抢红包大家都玩过，现在抢红包已经是我们每年过年的一个全民竞技体育了，每个人抢到那几分钱都特别地开心。

但有段时间我发现了一个奇怪的现象，就是不管别人发多大的红包，抢到我手里的每次都只有几分钱。而往往是抢红包比较晚的那些人，他们可以抢到一个比较大的红包。

这不科学吧？我说腾讯这么大的一个公司，它没有必要在算法上针对我呀。难道微信红包先抢和后抢的规律是不一样的？想到这个想法我非常地兴奋，我觉得如果我最后能找到这个规律的话，我就能抢到我所有的同学都破产为止。

马上又开始实验了。我在周围借来了四部手机，连上我自己的一部，总共是五部手机，建了个五人群开始发红包。发红包之前我先做了这么一个先导实验：N个人抢N+1分钱。

大家都学过抽屉原理，N个人抢N+1分钱就应该有一个人抢到2分钱，剩下的人都抢到1分钱。但实际做出来实验结果不是这样的，永远只有最后那个人才能抢到那个2分钱。

我做了非常多次实验，结果肯定是对的。这个东西我把它命名为末位红包抽屉原理。也就是N个人抢N+1分钱，则必有最后一个人抢到2分钱。这个收益率很可怕，他的收益率达到了前面一个人的两倍。

这个结果虽然很简单，但是它反映出来一个现象，就是微信红包的内部算法肯定不是均匀的，先抢后抢一定是有区别的，而且貌似后抢会占一点点优势。

究竟是不是这样呢？我做了一个进一步的实验。

我用5个人抢50块钱的红包，发了150次，然后统计了每一次这5个人的数据，得到这样750个数据。我把750个数据做在一张表上面。

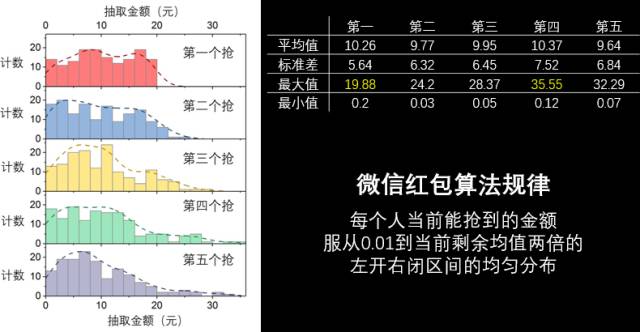
大家可以看出来，很惊讶的一个结果：5个人抢50块钱的红包，第一个人从来没有超过20块钱。做了150次，所以统计规律肯定是没有问题的。第二个人从来没有超过过25块钱，等到第三第四第五的人他们能抢到的钱数慢慢才上去。

如果我们做一个统计学的分析，从平均值上来看，其实5个人抢到的钱差不多，都是在10块钱左右，5个人抢50块钱嘛。但如果从它的标准差，就是一个波动的情况，你会发现标准差越来越大。也就说第一个人可能只能抢到0到20，第四第五的人才能抢到0到50中间的任一个数字。

后来经过我仔细地研究，我终于发现了微信红包内部的算法规则是什么，每个人当前能抢到的金额服从一个0.01到当前剩余均值两倍的左开右闭区间的均匀分布。

什么意思呢？大概是说，5个人抢50块钱，那平均每个人能抢到10块钱。这个时候，第一个人抢的时候，他就只能抢到0—10×2也就是20块钱。你想第一个人多不巧，他只抢到了2块钱。那接下来的问题就变成了4个人抢48块钱，这个时候平均每个人能抢到12块钱。12的两倍是24，第二个人最大能抢到就变成24块钱。所以这个区间是一个不断放大的过程。

最后等我发现了这个规律之后，你就可以做一些很无聊的脑洞。比如说你可以编程给自己发红包，然后有一天我就给自己发了五千万个红包，得出来这样一个规律。

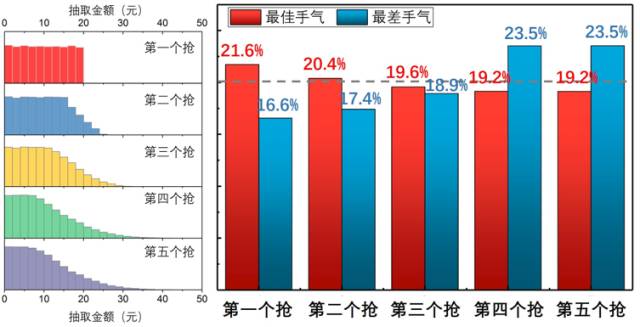
在五千万个红包下面这个规律就非常地明显了。你可以看到第1个人永远不会超过20，后面的这个规律分布在慢慢平缓下来。

此外，通过编程你还可以统计一个现象，就是最佳手气，这是很多人关注的一个点。最佳手气在各个人各个位置的概率是均等的吗？其实也不是。最后我发现最佳手气的概率在5个人抢的时候是依次递减的。

然后我的脑洞又发散了一下，我说难道5个人是这样，那几个人抢都是这样吗？于是我又做了一个编程，很无聊，就给自己发了两亿个红包。最后做出来这样一张图。

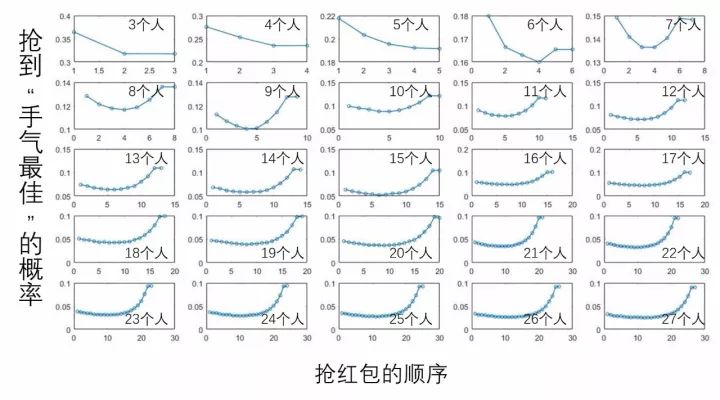
这张图可以说是微信抢红包里面包罗万象，它把所有的情况都概括了。它统计出了从3个人抢到27个人抢，如果你愿意的话，我可以统计到任何多个人抢。从3个人到27个人，不同的人在抢红包的时候，每一个位置抢到手气最佳的概率这个变化究竟是什么样子的。

从这张图的最后我大概得出一个结论，就是通常抢红包的人比较多的时候，应该是越往后往往抢到手气最佳的概率越大。所以以后我看到红包都先憋一会儿，我等你们先把前面的小红包都抢走了，憋到后面我再去把那个大的捞回来。

后来在这种思想的指导下，我就再也没有抢到过红包。